Hexagonal trapezohedron
In geometry, a hexagonal trapezohedron or deltohedron is the fourth in an infinite series of trapezohedra which are dual polyhedron to the antiprisms. It has twelve faces which are congruent kites.
| Hexagonal trapezohedron | |
|---|---|
 | |
| Type | trapezohedra |
| Conway | dA6 |
| Coxeter diagram | |
| Faces | 12 kites |
| Edges | 24 |
| Vertices | 14 |
| Face configuration | V6.3.3.3 |
| Symmetry group | D6d, [2+,12], (2*6), order 24 |
| Rotation group | D6, [2,6]+, (66), order 12 |
| Dual polyhedron | hexagonal antiprism |
| Properties | convex, face-transitive |
It is a isohedral figure, (face-transitive), having all its faces the same. More specifically, all faces must be not merely congruent but must be transitive, i.e. must lie within the same symmetry orbit. Convex isohedral polyhedra are the shapes that will make fair dice.[1]
Symmetry
The symmetry a hexagonal trapezohedron is D6d of order 24. The rotation group is D6 of order 12.
Variations
One degree of freedom within D6 symmetry changes the kites into congruent quadrilaterals with 3 edges lengths. In the limit, one edge of each quadrilateral goes to zero length, and these become bipyramids.
Crystal arrangements of atoms can repeat in space with hexagonal trapezohedral cells.[2]
If the kites surrounding the two peaks are of different shapes, it can only have C6v symmetry, order 12. These can be called unequal trapezohedra. The dual is an unequal antiprism, with the top and bottom polygons of different radii. If it twisted and unequal its symmetry is reduced to cyclic symmetry, C6 symmetry, order 6.
| Type | Twisted trapezohedra (isohedral) | Unequal trapezohedra | Unequal and twisted | |
|---|---|---|---|---|
| Symmetry | D6, (662), [6,2]+, order 12 | C6v, (*66), [6], order 12 | C6, (66), [6]+, order 6 | |
| Image (n=6) |
 |
 |
 |
 |
| Net | 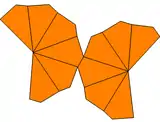 |
 |
 |
 |
Spherical tiling
The hexagonal trapezohedron also exists as a spherical tiling, with 2 vertices on the poles, and alternating vertices equally spaced above and below the equator.
Related polyhedra
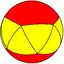
| Uniform hexagonal dihedral spherical polyhedra | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [6,2], (*622) | [6,2]+, (622) | [6,2+], (2*3) | ||||||||||||
 |
 |
 |
 |
 |
 |
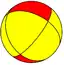 | ||||||||
| {6,2} | t{6,2} | r{6,2} | t{2,6} | {2,6} | rr{6,2} | tr{6,2} | sr{6,2} | s{2,6} | ||||||
| Duals to uniforms | ||||||||||||||
 |
 |
 |
 |
 |
 |
 |
 |
 | ||||||
| V62 | V122 | V62 | V4.4.6 | V26 | V4.4.6 | V4.4.12 | V3.3.3.6 | V3.3.3.3 | ||||||
| Trapezohedron name | Digonal trapezohedron (Tetrahedron) |
Trigonal trapezohedron | Tetragonal trapezohedron | Pentagonal trapezohedron | Hexagonal trapezohedron | Heptagonal trapezohedron | Octagonal trapezohedron | Decagonal trapezohedron | Dodecagonal trapezohedron | ... | Apeirogonal trapezohedron |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Polyhedron image |  |
 |
 |
 |
 |
 |
 |
 |
... | ||
| Spherical tiling image |  |
 |
 |
 |
 |
 |
 |
 |
Plane tiling image | ||
| Face configuration | V2.3.3.3 | V3.3.3.3 | V4.3.3.3 | V5.3.3.3 | V6.3.3.3 | V7.3.3.3 | V8.3.3.3 | V10.3.3.3 | V12.3.3.3 | ... | V∞.3.3.3 |
References
- McLean, K. Robin (1990), "Dungeons, dragons, and dice", The Mathematical Gazette, 74 (469): 243–256, doi:10.2307/3619822, JSTOR 3619822.
- 3 2 and Hexagonal-trapezohedric Class, 6 2 2
External links
- Weisstein, Eric W. "Trapezohedron". MathWorld.
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra