Vector (mathematics and physics)
In mathematics and physics, a vector is an element of a vector space. For many specific vector spaces, the vectors have received specific names, which are listed below. In general, a Euclidean vector is a geometric object with both length and direction, which is frequently represented as an arrow which starting point is arbitrary and thus chosen for convenience. Such vectors can be added to each other or scaled using vector algebra. Correspondingly, an ensemble of vectors is called a vector space. These objects are the subject of linear algebra and can be characterized by their dimension.
Historically, vectors were introduced in geometry and physics (typically in mechanics) before the formalization of the concept of a vector space. (In fact, the Latin word vector means "carrier".) Therefore, one often talks about vectors without specifying the vector space to which they belong. Specifically, in a Euclidean space, one considers spatial vectors, also called Euclidean vectors which are used to represent quantities that have both magnitude and direction, and may be added, subtracted and scaled (i.e. multiplied by a real number) for forming a vector space.[1]
Vectors in Euclidean geometry

In mathematics, physics and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector[2] or spatial vector[3]) is a geometric object that has magnitude (or length) and direction. Vectors can be added to other vectors according to vector algebra. A Euclidean vector is frequently represented by a directed line segment, or graphically as an arrow connecting an initial point A with a terminal point B,[4] and denoted by .
A vector is what is needed to "carry" the point A to the point B; the Latin word vector means "carrier".[5] It was first used by 18th century astronomers investigating planetary revolution around the Sun.[6] The magnitude of the vector is the distance between the two points, and the direction refers to the direction of displacement from A to B. Many algebraic operations on real numbers such as addition, subtraction, multiplication, and negation have close analogues for vectors,[7] operations which obey the familiar algebraic laws of commutativity, associativity, and distributivity. These operations and associated laws qualify Euclidean vectors as an example of the more generalized concept of vectors defined simply as elements of a vector space.
Vectors play an important role in physics: the velocity and acceleration of a moving object and the forces acting on it can all be described with vectors.[8] Many other physical quantities can be usefully thought of as vectors. Although most of them do not represent distances (except, for example, position or displacement), their magnitude and direction can still be represented by the length and direction of an arrow. The mathematical representation of a physical vector depends on the coordinate system used to describe it. Other vector-like objects that describe physical quantities and transform in a similar way under changes of the coordinate system include pseudovectors and tensors.[9]Vector spaces
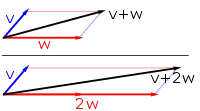
In mathematics, physics, and engineering, a vector space (also called a linear space) is a set whose elements, often called vectors, may be added together and multiplied ("scaled") by numbers called scalars. Scalars are often real numbers, but can be complex numbers or, more generally, elements of any field. The operations of vector addition and scalar multiplication must satisfy certain requirements, called vector axioms. The terms real vector space and complex vector space are often used to specify the nature of the scalars.
Vector spaces generalize Euclidean vectors, which allow modeling physical quantities, such as forces and velocity, that have not only a magnitude, but also a direction. The concept of vector spaces is fundamental for linear algebra, together with the concept of matrix, which allows computing in vector spaces. This provides a concise and synthetic way for manipulating and studying systems of linear equations.
Vector spaces are characterized by their dimension, which, roughly speaking, specifies the number of independent directions in the space. This means that, for two vector spaces with the same dimension, the properties that depend only from the vector-space structure are exactly the same (technically the vector spaces are isomorphic). A vector space is finite-dimensional if its dimension is a natural number. Otherwise, it is infinite-dimensional, and its dimension is an infinite cardinal. Finite-dimensional vector spaces occur naturally in geometry and related areas. Infinite-dimensional vector spaces occur in many areas of mathematics. For example, polynomial rings are countably infinite-dimensional vector spaces, and many function spaces have the cardinality of the continuum as a dimension.
Many vector spaces that are considered in mathematics are also endowed with other structures. This is the case of algebras, which include field extensions, polynomial rings, associative algebras and Lie algebras. This is also the case of topological vector spaces, which include function spaces, inner product spaces, normed spaces, Hilbert spaces and Banach spaces.Concepts related to vector spaces
- Specific vectors in a vector space
- Zero vector (sometimes also called null vector and denoted by ), the additive identity in a vector space. In a normed vector space, it is the unique vector of norm zero. In a Euclidean vector space, it is the unique vector of length zero.[10]
- Basis vector, an element of a given basis of a vector space.
- Unit vector, a vector in a normed vector space whose norm is 1, or a Euclidean vector of length one.[10]
- Isotropic vector or null vector, in a vector space with a quadratic form, a non-zero vector for which the form is zero. If a null vector exists, the quadratic form is said an isotropic quadratic form.
- Vectors in specific vector spaces
- Column vector, a matrix with only one column. The column vectors with a fixed number of rows form a vector space.
- Row vector, a matrix with only one row. The row vectors with a fixed number of columns form a vector space.
- Coordinate vector, the n-tuple of the coordinates of a vector on a basis of n elements. For a vector space over a field F, these n-tuples form the vector space (where the operation are pointwise addition and scalar multiplication).
- Displacement vector, a vector that specifies the change in position of a point relative to a previous position. Displacement vectors belong to the vector space of translations.
- Position vector of a point, the displacement vector from a reference point (called the origin) to the point. A position vector represents the position of a point in a Euclidean space or an affine space.
- Velocity vector, the derivative, with respect to time, of the position vector. It does not depend of the choice of the origin, and, thus belongs to the vector space of translations.
- Pseudovector, also called axial vector
- Covector, an element of the dual of a vector space. In an inner product space, the inner product defines an isomorphism between the space and its dual, which may make difficult to distinguish a covector from a vector. The distinction becomes apparent when one changes coordinates (non-orthogonally).
- Tangent vector, an element of the tangent space of a curve, a surface or, more generally, a differential manifold at a given point (these tangent spaces are naturally endowed with a structure of vector space)
- Normal vector or simply normal, in a Euclidean space or, more generally, in an inner product space, a vector that is perpendicular to a tangent space at a point.
- Gradient, the coordinates vector of the partial derivatives of a function of several real variables. In a Euclidean space the gradient gives the magnitude and direction of maximum increase of a scalar field. The gradient is a covector that is normal to a level curve.
- Four-vector, in the theory of relativity, a vector in a four-dimensional real vector space called Minkowski space
Vectors in algebras
Every algebra over a field is a vector space, but elements of an algebra are generally not called vectors. However, in some cases, they are called vectors, mainly due to historical reasons.
- Vector quaternion, a quaternion with a zero real part
- Multivector or p-vector, an element of the exterior algebra of a vector space.
- Spinors, also called spin vectors, have been introduced for extending the notion of rotation vector. In fact, rotation vectors represent well rotations locally, but not globally, because a closed loop in the space of rotation vectors may induce a curve in the space of rotations that is not a loop. Also, the manifold of rotation vectors is orientable, while the manifold of rotations is not. Spinors are elements of a vector subspace of some Clifford algebra.
- Witt vector, an infinite sequence of elements of a commutative ring, which belongs to an algebra over this ring, and has been introduced for handling carry propagation in the operations on p-adic numbers.
Data represented by vectors
The set of tuples of n real numbers has a natural structure of vector space defined by component-wise addition and scalar multiplication. It is common to call these tuples vectors, even in contexts where vector-space operations do not apply. More generally, when some data can be represented naturally by vectors, they are often called vectors even when addition and scalar multiplication of vectors are not valid operations on these data. Here are some examples.
- Rotation vector, a Euclidean vector whose direction is that of the axis of a rotation and magnitude is the angle of the rotation.
- Burgers vector, a vector that represents the magnitude and direction of the lattice distortion of dislocation in a crystal lattice
- Interval vector, in musical set theory, an array that expresses the intervallic content of a pitch-class set
- Probability vector, in statistics, a vector with non-negative entries that sum to one.
- Random vector or multivariate random variable, in statistics, a set of real-valued random variables that may be correlated. However, a random vector may also refer to a random variable that takes its values in a vector space.
- Logical vector, a vector of 0s and 1s (Booleans).
See also
| Look up vector in Wiktionary, the free dictionary. |
Vector spaces with more structure
- Graded vector space, a type of vector space that includes the extra structure of gradation
- Normed vector space, a vector space on which a norm is defined
- Hilbert space
- Ordered vector space, a vector space equipped with a partial order
- Super vector space, name for a Z2-graded vector space
- Symplectic vector space, a vector space V equipped with a non-degenerate, skew-symmetric, bilinear form
- Topological vector space, a blend of topological structure with the algebraic concept of a vector space
Vector fields
A vector field is a vector-valued function that, generally, has a domain of the same dimension (as a manifold) as its codomain,
- Conservative vector field, a vector field that is the gradient of a scalar potential field
- Hamiltonian vector field, a vector field defined for any energy function or Hamiltonian
- Killing vector field, a vector field on a Riemannian manifold
- Solenoidal vector field, a vector field with zero divergence
- Vector potential, a vector field whose curl is a given vector field
- Vector flow, a set of closely related concepts of the flow determined by a vector field
Miscellaneous
- Ricci calculus
- Vector Analysis, a textbook on vector calculus by Wilson, first published in 1901, which did much to standardize the notation and vocabulary of three-dimensional linear algebra and vector calculus
- Vector bundle, a topological construction that makes precise the idea of a family of vector spaces parameterized by another space
- Vector calculus, a branch of mathematics concerned with differentiation and integration of vector fields
- Vector differential, or del, a vector differential operator represented by the nabla symbol
- Vector Laplacian, the vector Laplace operator, denoted by , is a differential operator defined over a vector field
- Vector notation, common notation used when working with vectors
- Vector operator, a type of differential operator used in vector calculus
- Vector product, or cross product, an operation on two vectors in a three-dimensional Euclidean space, producing a third three-dimensional Euclidean vector
- Vector projection, also known as vector resolute or vector component, a linear mapping producing a vector parallel to a second vector
- Vector-valued function, a function that has a vector space as a codomain
- Vectorization (mathematics), a linear transformation that converts a matrix into a column vector
- Vector autoregression, an econometric model used to capture the evolution and the interdependencies between multiple time series
- Vector boson, a boson with the spin quantum number equal to 1
- Vector measure, a function defined on a family of sets and taking vector values satisfying certain properties
- Vector meson, a meson with total spin 1 and odd parity
- Vector quantization, a quantization technique used in signal processing
- Vector soliton, a solitary wave with multiple components coupled together that maintains its shape during propagation
- Vector synthesis, a type of audio synthesis
Notes
- "vector | Definition & Facts". Encyclopedia Britannica. Retrieved 2020-08-19.
- Ivanov 2001
- Heinbockel 2001
- Itô 1993, p. 1678; Pedoe 1988
- Latin: vectus, perfect participle of vehere, "to carry"/ veho = "I carry". For historical development of the word vector, see "vector n.". Oxford English Dictionary (Online ed.). Oxford University Press. (Subscription or participating institution membership required.) and Jeff Miller. "Earliest Known Uses of Some of the Words of Mathematics". Retrieved 2007-05-25.
- The Oxford english dictionary (2nd. ed.). London: Claredon Press. 2001. ISBN 9780195219425.
- "vector | Definition & Facts". Encyclopedia Britannica. Retrieved 2020-08-19.
- "Vectors". www.mathsisfun.com. Retrieved 2020-08-19.
- Weisstein, Eric W. "Vector". mathworld.wolfram.com. Retrieved 2020-08-19.
- Weisstein, Eric W. "Vector". mathworld.wolfram.com. Retrieved 2020-08-19.
References
- Heinbockel, J. H. (2001). Introduction to Tensor Calculus and Continuum Mechanics. Trafford Publishing. ISBN 1-55369-133-4.
- Itô, Kiyosi (1993). Encyclopedic Dictionary of Mathematics (2nd ed.). MIT Press. ISBN 978-0-262-59020-4.
- Ivanov, A.B. (2001) [1994], "Vector", Encyclopedia of Mathematics, EMS Press
- Pedoe, Daniel (1988). Geometry: A comprehensive course. Dover. ISBN 0-486-65812-0.